与陆上风电场相比,海上风电机组基础结构重心高、水平荷载和倾覆弯矩大,同时还要考虑波浪、海流、海床地质及海冰等环境影响因素,因此,重力式基础是海上风电机组基础结构中的主要基础形式之一,具有陆上预制建造、无需海上打桩作业、节省施工时间和费用的特点,在施工便利性和工程成本控制方面都表现出较大的优越性。海上风电机组重力式基础主要依靠基础及内部压载物重量抵抗上部风电机组荷载和外部环境荷载产生的倾覆力矩和滑动力,使风电机组基础和塔架结构保持稳定。因此,基础稳定性计算是海上风电机组重力式基础设计的重要环节。
上海勘测设计研究院有限公司
杨威* 林毅峰
来源:《太阳能》杂志2019 年第5 期( 总第301 期)P78-74
由于我国海上风电开发建设起步较晚,海上风电基础设计规范尚处于编制和征求意见阶段;相比较而言,欧洲海上风电场的规划建设已进入大规模开发时期,海上风电工程设计经验丰富,配套的设计规范较为完善。对于海上风电机组重力式基础的稳定性计算,国内目前主要借鉴JTS 167-2-2009《重力式码头设计与施工规范》[1]、GB 50135-2006《高耸结构设计规范》[2]、FD 003-2007《风电机组地基基础设计规定》[3] 等国内规范[4-5],以及国外的DNV规范[6]、API 规范[7] 和GL 规范[8]。但由于国内外规范之间存在差异,导致重力式基础设计存在标准不统一、安全系数不一致的问题。本文通过对比国内外规范中关于重力式基础稳定性计算方法之间的差异,分析了重力式基础稳定性计算的理论和方法,为海上风电机组重力式基础的设计提供更加经济适用的计算方法和技术标准。
1 重力式基础稳定性计算模型
海上风电机组重力式基础需要承受来自各个方向的大偏心荷载,基础底板一般设计为对称的多边形或圆( 环) 形,本文以圆形底板为例进行分析。图1 为浅水海域重力式基础的典型结构,由混凝土底板、圆柱段壳体、抗冰锥和工作平台组成,基础顶部与风电机组塔筒连接,抗冰锥设置于海平面附近,基础安装在经过整平的碎石垫层上。
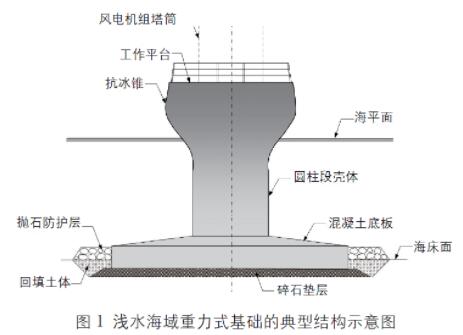
作用在重力式基础基底上的荷载主要包括上部结构传递过来的竖向力N,基础自重G,由上部风电机组、波浪和海流引起的水平力H,弯矩M,扭矩T,静水压力,基床反力,基床摩擦力等。海上风电机组重力式基础稳定性计算主要包括地基承载力、基础抗倾覆稳定及基础抗滑移稳定3 个部分的设计内容。值得注意的是,DNV 规范[6] 对重力式基础受到扭矩作用时有特殊的条文规定:在计算地基承载力时,需要将扭矩作用经给定的公式转换成等效的水平荷载;而在我国规范中,尚未考虑扭矩荷载对重力式基础的影响。
2 地基承载力的计算方法对比
地基承载力计算包括基底反力计算和基床承载力计算两部分。对于基底反力计算,我国GB50135-2006《高耸结构设计规范》[2] 中假设基底反力呈线性分布,规定正常使用状态下荷载效应的标准组合不允许脱开地基土,极限状态下底面允许脱开地基土的面积不大于底面全面积的25%,偏心荷载在基础底面产生的偏心比e/R 的计算式为:

式中,e 为偏心距;R 为基础底板半径;Nk为上部结构传至基础的竖向力标准值;Gk 为基础自重标准值;Mk 为上部结构传至基底的力矩标准值。
根据我国规范,重力式基础的脱开面积A 的计算式为:

式中,θ 为脱开部分对应的圆弧半角。

式中,l 为脱开部分的宽度。表1 为基底允许偏心比及脱开面积百分比取值,图2 为重力式基础基底脱开及基底反力p 的示意图。
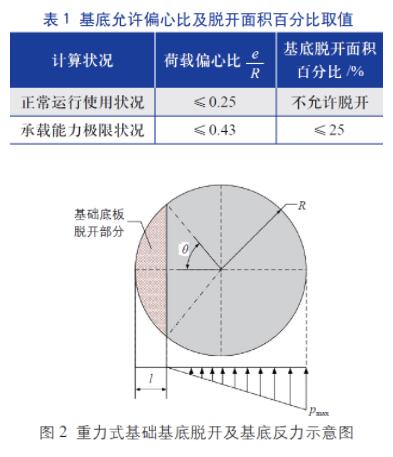
不同于我国规范中习惯采用线弹性理论的假设,国外的DNV 规范[6] 和API 规范[7] 中都采用了塑性土压力分布理论,把基础承受的偏心荷载转换成有效受压面内的均布力,如图3所示。图中,D 为基底的直径。
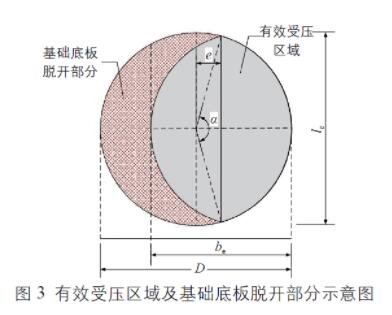
有效受压区域可等效为矩形区域尺寸,计算式为:

式中,Aeff 为有效受压区域的面积;leff 为等效矩形的长度;beff 为等效矩形的宽度;le 为有效受压区域的长度;be 为有效受压区域的宽度。根据DNV 规范[6],重力式基础的脱开面积A 可表示为:

式中,α 为有效受压区域对应的圆心角。
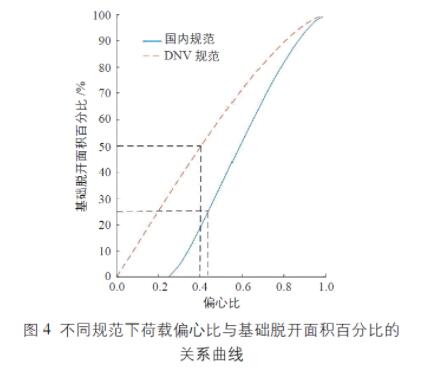
图4 给出了不同规范中荷载偏心比e/R 与基础的脱开面积百分比的关系曲线。由于DNV 规范采用塑性土压力分布理论计算基础的有效受压区域,导致在相同荷载偏心比下,其计算的基础脱开面积百分比要大于根据《高耸结构设计规范》计算的结果。出现这种差异是由于两种规范计算脱开面积采用的理论不同导致的,德国风电机组基础设计标准GL 2010 规范[8] 和DIN 1054 标准[9] 规定:重力式基础在极端荷载工况下允许有50%的基础底部面积脱开。但从图4 可以看出,在DNV 规范[6] 中,基础底部脱开面积为50% 时对应的荷载偏心比为0.40;而在我国《高耸结构设计规范》[2] 中,基础底部脱开面积为25% 时对应的荷载偏心比为0.43,所以,两种规范关于基础底部脱开面积大小的规定其实是相当的。

对于地基承载力,我国规范[2,5] 根据平板荷载试验或其他原位测试、公式计算,并结合工程实践经验等方法综合确定,同时按照基础宽度、埋置深度和基床土体的类别进行修正。而国外规范,如DNV 规范[6] 和API 规范[7],主要根据Vesic 地基承载力理论公式进行计算,根据土体的抗剪强度指标确定地基承载力的Vesic 公式适用条件为均布压力。然而当风电机组基础受到较大的水平荷载而使合力的偏心距过大时,地基反力分布很不均匀,因此,我国规范中确定地基承载力的方法更简便实用。
3 基础抗倾覆稳定的计算方法对比
国内关于重力式基础的抗倾覆稳定验算主要参照JTS 167-2-2009《重力式码头设计与施工规范》[1]、GB 50135-2006《高耸结构设计规范》[2]、FD 003-2007《风电机组地基基础设计规定》[3]。其中,《高耸结构设计规范》特别说明:当基础底面脱开地基土的面积不大于全部面积的1/4,且满足地基承载力要求时,可不验算基础的倾覆稳定性。实际上,当脱开地基土的面积比为25% 时,对应的荷载偏心比为0.43,计算公式见式(1)。
根据陆上风电机组的《风电机组地基基础设计规定》[3] 的要求,基础底板边缘的抗倾覆稳定计算式为:
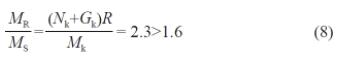
式中,MR 为荷载效应基本组合下的抗倾覆力矩;MS 为荷载效应基本组合下的倾覆力矩。由式(8) 的计算结果可以看出,当基础底面脱开地基土的面积不大于全部面积的25% 时,基础的抗倾覆稳定能够自动满足规范要求的安全系数,这也能够说明《高耸结构设计规范》特意强调“基底脱空面积不超过25% 时可不验算基础的倾覆稳定性”的原因。
而按照港口码头工程《重力式码头设计与施工规范》[1] 的要求,基础的抗倾覆稳定计算式为:

式中,γ0 为结构重要性系数。需要说明的是,上述分项系数表达的概率极限状态设计方法是按照安全系数K=1.6 的单一安全系数法进行校准的。也就是说,陆上风电机组的《风电机组地基基础设计规定》与港口码头工程的《重力式码头设计与施工规范》关于抗倾覆稳定的设计安全度是相当的。
国外的DNV 规范[6] 和API 规范[7] 未对重力式基础抗倾覆稳定计算进行条文规定,主要是由于抗倾覆稳定实际上已经包含在地基承载力计算的规定中。也就是说,当重力式基础满足地基承载力的计算要求时,抗倾覆稳定能够自动满足。
4 基础抗滑移稳定的计算方法对比
国内关于重力式基础的抗滑移稳定计算同样主要参照JTS 167-2-2009《重力式码头设计与施工规范》[1]、GB 50135-2006《高耸结构设计规范》[2]和FD 003-2007《风电机组地基基础设计规定》[3]。《高耸结构设计规范》中规定,基础抗滑移稳定按式(10) 计算:

式中,FR 为荷载效应基本组合下的抗滑力;FS 为荷载效应基本组合下的滑动力;Hk 为水平力标准值;μ 为基础底面对地基的摩擦系数。《重力式码头设计与施工规范》[1] 中的抗滑移稳定计算式为:

需要强调的是,上述分项系数表达的概率极限状态设计方法是按照安全系数K=1.3 的单一安全系数法进行校准的,这与《高耸结构设计规范》、《风电机组地基基础设计规定》中的安全度是一致的。
国外的DNV 规范[6] 和API 规范[7] 中规定,在重力式基础受水平荷载作用时,必须对基础抗滑移稳定进行验算,具体计算为:
式中,c 为滑动面的粘聚力;φ 为滑动面的摩擦角;r 为粗糙系数,接触面材料为土体- 土体时取值为1.0,接触面材料为结构-土体时取值小于1.0。与国内规范相比,国外规范中的基础抗滑移稳定计算公式考虑了滑动面粘聚力的影响,同时引入了粗糙系数来区别不同滑动面材料对安全系数的要求,且粗糙系数的取值比较灵活。其他方面两种规范体系大体类似,都包括用竖向力乘以摩擦系数作为抗滑力。
5 工程实例
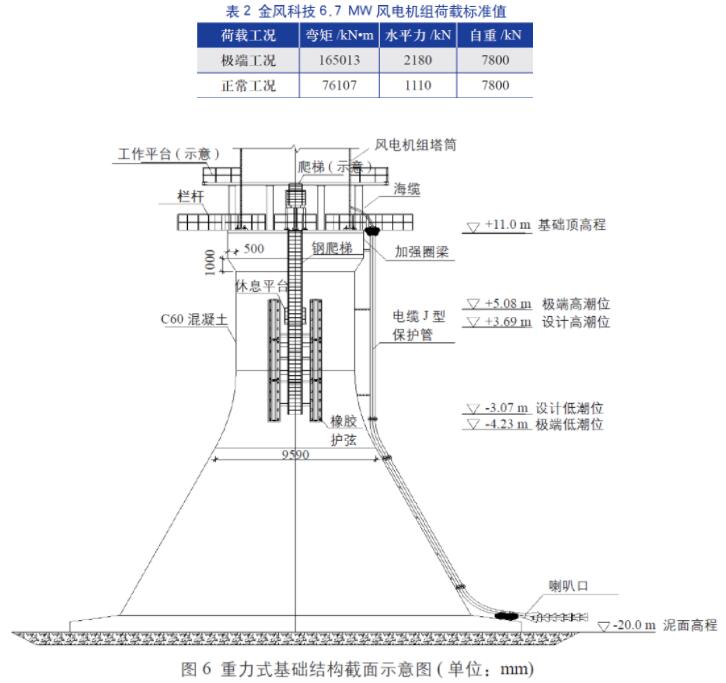
以福建省某海上风电场为例对分析结论进行验证。该风电场地质条件为浅覆盖层,地基承载力特征值fak 为250 kPa,采用金风科技6.7 MW抗台风大容量风电机组,基础形式拟采用重力式基础,基础截面如图6 所示。

分别按照国内和国外规范对该风电场的重力式基础进行设计,具体承载力和稳定性计算结果如表3、表4 所示。
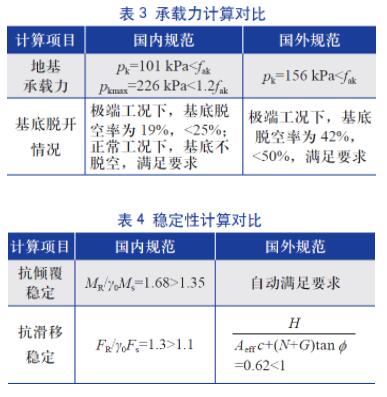
从表3、表4 可以看出,按照国内外规范得出的地基承载力、基础抗倾覆稳定和基础抗滑移稳定的计算结果都可满足规范的要求,验证了上述分析结论。
6 结论
本文通过研究国内外规范中关于海上风电机组重力式基础稳定性的计算理论和方法,对重力式基础的地基承载力、基础抗倾覆稳定及基础抗滑移稳定的计算方法进行了详细的对比分析,并对国内外规范中给出的计算理论的优劣和条文说明进行了论述,得到结论如下:
1) 我国规范中,习惯采用线弹性理论计算地基承载力,而国外规范倾向于采用塑性土压力分布理论。国外规范中,基础底部面积50% 脱开对应的荷载偏心比e/R 为0.40;我国规范中,基础底部面积25% 脱开对应的荷载偏心比e/R 为0.43,两种规范关于底面积脱开大小的规定实质是相当的。
2) 我国规范根据荷载试验并结合工程实践经验等方法综合确定基础承载力;而国外规范采用的Vesic 基础承载力公式适用条件为均布压力,当基础受到较大的水平荷载时会引起地基反力分布不均匀,计算结果会出现较大偏差。
3) 我国规范专门强调基底脱开面积不超过25% 且满足地基承载力要求时,可不验算基础的抗倾覆稳定性;国外规范中没有规定必须对基础抗倾覆稳定进行计算,主要原因是抗倾覆稳定实际上已经包含在地基承载力计算的规定中。
4) 与国内规范相比,国外规范中的基础抗滑移稳定计算公式考虑了滑动面粘聚力的影响,同时引入了粗糙系数以区别不同滑动面材料对安全系数的要求。